Moroccan Traditions
Published on

Elliptic Curve Cryptography Powering Modern Asymmetric Encryption

Authors
  • avatar
    Name
    Adil ABBADI
    Twitter

Introduction

In the realm of cryptography, asymmetric encryption has emerged as a powerful tool for securing online transactions, communication, and data exchange. At the heart of this security lies elliptic curve cryptography (ECC), a mathematical framework that has revolutionized the way we approach encryption and decryption. In this article, we'll embark on a journey to explore the intricacies of ECC, its advantages, and its widespread applications in modern cryptography.

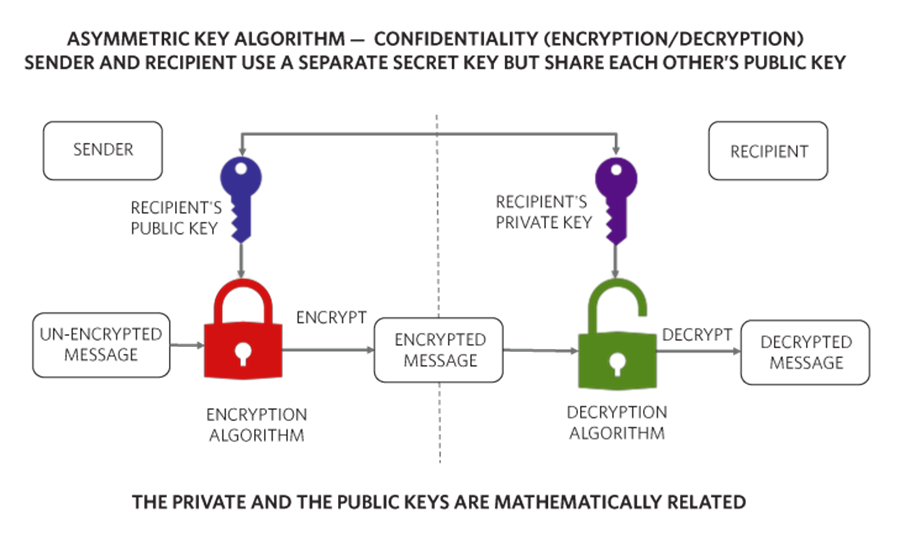
Graphical representation of an elliptic curve

What is Elliptic Curve Cryptography?

Elliptic curve cryptography is a type of public-key cryptography that uses the mathematical properties of elliptic curves to create a secure key exchange. The concept of elliptic curves dates back to the 19th century, but it wasn't until the 1980s that cryptographers began to explore its potential in cryptography.

In essence, ECC relies on the difficulty of the elliptic curve discrete logarithm problem (ECDLP), which makes it challenging to compute the discrete logarithm of a random elliptic curve element. This problem is analogous to the difficulty of computing the discrete logarithm in a finite field, which is the foundation of other public-key cryptosystems like RSA.

Key Pair Generation

In ECC, a key pair consists of a private key and a corresponding public key. The private key is used for decryption and signature generation, while the public key is used for encryption and verification.

To generate a key pair, you need to follow these steps:

  1. Select a suitable elliptic curve and its corresponding parameters.
  2. Choose a random private key d from the interval [1, n-1], where n is the order of the curve.
  3. Compute the public key Q by multiplying the base point G with the private key d: Q = d * G.
import ecdh

# Select a suitable elliptic curve (e.g., secp256k1)
curve = ecdh.Curve('secp256k1')

# Choose a random private key
d = 0x1234567890abcdef

# Compute the public key
Q = d * curve.G

Advantages of Elliptic Curve Cryptography

Elliptic curve cryptography offers several advantages over other public-key cryptosystems:

Smaller Key Sizes

ECC key sizes are significantly smaller than those of other cryptosystems, making them more efficient in terms of storage and transmission. For example, a 256-bit ECC key provides the same level of security as a 3072-bit RSA key.

Faster Performance

ECC operations are generally faster than those of other cryptosystems, particularly when it comes to key exchange and signature verification.

Better Security

ECC is considered more secure than other cryptosystems, given the difficulty of the ECDLP problem.

Key size comparison between ECC and RSA

Real-World Applications of Elliptic Curve Cryptography

Elliptic curve cryptography has numerous applications in modern cryptography, including:

Secure Web Browsing (TLS/SSL)

ECC is used in Transport Layer Security (TLS) and Secure Sockets Layer (SSL) protocols to establish secure connections between web browsers and servers.

Bitcoin and Cryptocurrencies

ECC is used in cryptocurrency protocols like Bitcoin to enable secure transactions and wallet management.

Secure Email Communication (PGP)

ECC is used in Pretty Good Privacy (PGP) to provide end-to-end encryption for secure email communication.

Internet of Things (IoT) Security

ECC is used in IoT devices to provide secure communication and data exchange between devices and the cloud.

Digital Signatures

ECC is used in digital signature schemes like ECDSA to provide authenticity and integrity of digital messages.

Conclusion

Elliptic curve cryptography has emerged as a powerful tool in modern asymmetric encryption, offering smaller key sizes, faster performance, and better security. Its widespread applications in secure web browsing, cryptocurrencies, secure email communication, IoT security, and digital signatures make it an essential component of our digital lives.

Final Call-to-Action

As the cryptographic landscape continues to evolve, it's essential to stay up-to-date with the latest developments in ECC and its applications. Explore the world of elliptic curve cryptography and discover its potential in powering modern asymmetric encryption.

Comments